Kan vi forutse epidemier?
POPULÆRVITENSKAP: Ny matematisk forskning forteller oss at sommermånedene inneholder skjult informasjon om framtiden.
Virussykdommer som influensa og dengue rammer millioner mennesker hvert år og fører til hundretusenvis av dødsfall. Dengue overføres mellom mennesker via mygg, og er utbredt i tropiske områder. Influensa, som smitter direkte mellom mennesker, er utbredt over hele verden, og svinger med årstidene på den nordlige og sørlige halvkule siden viruset smitter lettere ved lave temperaturer.
Vi kjenner alle til begrepet influensasesong, men det er ikke slik at alle influensasesonger er like. Noen år er vinterepidemien mer alvorlig enn normalt, som for eksempel vinteren 2008 da den såkalte svineinfluensaen rammet. Utbredelsen av dengue i tropiske strøk varierer på en liknende måte. De fleste steder er det en tydelig høysesong og betydelig variasjon i omfang fra år til år.
Hvis vi kan forutsi omfanget av neste års influensaepidemi eller dengueepidemi før den inntreffer vil det gi muligheter for allokering av ressurser til preventive tiltak. De siste tiårene er det forsket mye på matematiske og statistiske metoder for å gjøre slike prediksjoner. Det er utviklet modeller som tar høyde for klimatiske variasjoner, demografi og virusevolusjon. For dengue kommer hele økosystemet til de smittebærende myggartene også i betraktning.
Kompleks eller enkel modell?
Selv om alle disse faktorene vesentlige, så vil ikke nødvendigvis modeller med mange forklaringsvariabler gi bedre prediksjoner enn litt enklere modeller. Prosessene er svært komplekse og de er ikke er fullstendig forstått. I tillegg er modellene avhengige av faktorer som er vanskelig å kvantifisere.
De usikre elementene i modellene kan ikke fastslås ved hjelp av teoretiske betraktninger og må derfor bestemmes av observasjoner, som for eksempel tidsrekker av antall registrerte sykdomstilfeller per uke i et gitt geografisk område, eventuelt supplert med informasjon fra blodprøver av de sykdomsrammede. Statistikerne må bruke noen av observasjonene til å bestemme usikre modellparametere, og de resterende observasjonene til å vurdere hvor gode prediksjoner er. Dette kalles trening og validering.
Ofte vil resultatet av modelltreningen blir bestemt av tilfeldige variasjoner i observasjonsdata og ikke av de prosessene som man har ment å beskrive. Da spiller det liten rolle om de likningene man har skrevet ned er helt riktige. Derimot betyr det mye om man har laget en veldig kompleks modell. Hvis det er mange usikre parametere vil den generelt fungere dårlig for å gjøre prediksjoner av epidemier. Mer detaljert og mer nøyaktig modellering av det dynamiske systemet gir altså ikke nødvendigvis den ønskede effekten.
Hva med maskinlæring?
Som et alternativ til komplekse epidemiologiske modeller har det blitt stadig mer populært å bruke generelle metoder for automatisert modellkonstruksjon basert på observasjoner. Slike maskinlæringsalgoritmer innebærer ofte at en ikke skriver opp likninger for å beskrive hvordan et virus sprer seg i en befolkning, men i stedet identifiserer korrelasjoner mellom utvalgte forklaringsvariabler og det man ønsker å forklare. Sistnevnte vil i vårt tilfellet være størrelsen av en sensongepidemi målt i antall rammede individer i et gitt område.
Men slike metoder fungerer best hvis man har gode observasjonsdata over veldig lang tid. Med de data som er tilgjengelig for influensa og dengue er ikke denne framgangsmåten spesielt velegnet.
Ny metode som ikke avhenger av detaljene
I en nylig artikkel i tidsskriftet Nature Communications presenterer vi en ny ide om hvordan omfanget av en vinterepidemi kan forutses fra observasjonsdata i de foregående sommermånedene. Ideen tar utgangspunkt i en generell matematisk struktur i likningene som beskriver hvordan en smittsom sykdom sprer seg i en befolkning. Men i motsetning til andre metoder, så avhenger ikke denne ideen av detaljene i disse likningene. Dermed unngår man problemet med mange usikre parametere, og vi oppnår forbedrede prediksjoner.
Vi tenker oss at det dynamiske systemet som beskriver spredningen av et virus i en befolkning veksler mellom å være stabilt og ustabilt. I sommermånedene er de klimatiske forholdene ugunstige for sykdomsspredning, og systemet er stabilt. Det betyr at selv om det skulle oppstå en liten sommerepidemi, så vil den raskt dø ut.
Når de klimatiske forholdene endrer seg, og betingelsene for sykdomsspredning blir mer gunstige, blir systemet ustabilt og antall smittede vil vokse raskt. Hvor mange mennesker som blir rammet under en vinterepidemi avhenger hovedsakelig av hvor stor graden av immunitet i befolkningen er, som igjen avhenger av hvor mye det aktuelle viruset likner på de som har sirkulert i befolkningen i årene før. Det er altså denne størrelsen, hvor mange individer som har lav eller ingen immunitet til det aktuelle viruset, som er nøkkelstørrelsen hvis man ønsker å forutse omfanget av en epidemi.
Matematisk innsikt kan gi nye varslingssystemer
Hvordan kan man så få informasjon om denne størrelsen som ikke er direkte målbar, og som i stor grad avhenger av tilfeldige mutasjoner i virusets arvestoff? Det er her den matematiske innsikten kommer inn. I likningene som beskriver sykdomsspredning er det nemlig en universell egenskap at antallet ikke-immune individer er tilnærmet proporsjonal med noe som kalles den ledende egenverdien til det sykdomsfrie likevektspunktet. Dette er en størrelse som karakteriserer hvor stabil en sykdomsfri sommer er. Med andre ord hvor fort en miniepidemi på sommeren dør ut.
Egenverdien kan enkelt beregnes løpende for tidsrekker av sykdomstilfeller og gjennomsnittet for sommermånedene gir et mål for graden av immunitet i befolkningen.
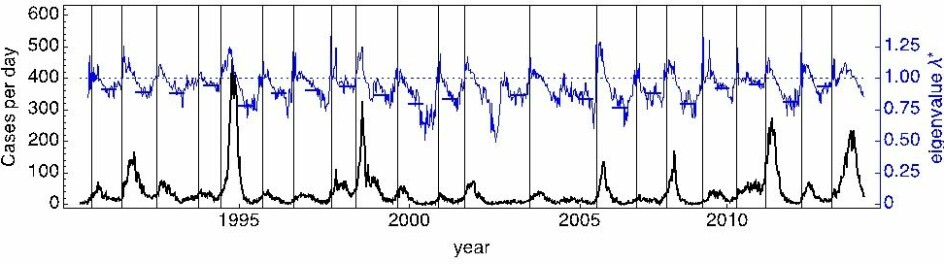
Figuren under viser en tidsrekke for antall tilfeller per uke av dengue i San Juan, Puerto Rico (svart kurve). Vi ser tydelige sesongepidemier av varierende størrelse. Den blå kurven er den omtalte egenverdien beregnet forløpende fra observasjonsdata, og de horisontale blå linjene er gjennomsnittsverdier for sommermånedene. De vertikale linjene indikerer tidspunktene på høsten der dynamikken går fra å være stabil til å være ustabil. Vi kan tydelig se at høye egenverdier svarer til at mange mennesker blir rammet av dengue den påfølgende vinteren.
Vi ser for oss at resultatene som er presentert i artikkelen vår vil bidra til utvikling av nye systemer for varsling, overvåkning og prediksjon av smittsomme sykdommer. I tillegg illustrerer de at, til tross for den enorme utviklingen som skjer innenfor områder som vitenskapelig beregning og kunstig intelligens, at er det fortsatt viktig å kunne gjenkjenne struktur i modeller og systemer. Ved våre respektive institusjoner i Tromsø og San Diego fokuserer vi på å lære studentene generelle metoder for å angripe problemer av denne typen, på tvers av fagområder og disipliner. Vi kaller det anvendt matematikk.
Referanse: Martin Rypdal og George Sugihara. «Inter-outbreak stability reflects the size of the susceptible pool and forecasts magnitudes of seasonal epidemics.» Nature Communications, 30. mai 2019. DOI: 10.1038/s41467-019-10099-y




























